SVG od podstaw - ścieżki
Wcześniej zostało wprowadzone pojęcie ścieżki. W tym rozdziale omówię je szerzej. Ścieżka jest to kształt powstały z połączonych fragmentów linii, łuków i krzywych.
Do dokumentu wstawiamy ją za pomocą znacznika <path>. Znacznik ten ma atrybut d, w którym określamy za pomocą odpowiednich
liter sposób prowadzenia ścieżki. Każda ścieżka musi rozpoczynać się od komendy moveto (M).
Określa ona punkt (współrzędne x i y oddzielone spacją), w którym rozpoczyna się nasza ścieżka. Ścieżka może zawierać jedną lub więcej komend lineto (L),
która odpowiada za poprowadzenie linii prostej do określonego punktu. Komendy oddzielamy przecinkami. To przykład prostej ścieżki wykorzystującej komendy moveto i lineto.
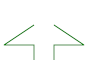
<?xml version="1.0"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1" xmlns:xlink="http://www.w3.org/1999/xlink"> <g style="stroke: green; fill: none;"> <path d="M 40 75, L 40 60, L 10 60, L 40 40, M 60 75, L 60 60, L 90 60, L 60 40" /> </g> </svg>Wyjaśnienie prowadzenia ścieżki od początku:
M 40 75 – startujemy w punkcie (40, 75).
L 40 60 – prowadzimy linię do punktu (40, 60).
L 10 60 – prowadzimy linię z poprzedniego punktu do (10, 60).
L 40 40 – prowadzimy linię do (40, 40).
M 60 75 – rozpoczynamy nową subścieżkę (kładziemy pióro w punkcie (60, 75), żadna linia nie jest rysowana).
L 60 60 – rysujemy linię do punktu (60, 60).
L 90 60 – prowadzimy linię do (90, 60).
L 60 40 – linia do (60, 40).
Teraz opiszę komendę closepath (Z). Jeśli chcemy przy użyciu <path> narysować np. Prostokąt to musimy narysować wszystkie cztery jego boki lub trzy i użyć komendy closepath (Z) czyli zamknięcię ścieżki. Poniższy przykład ilustruje użycie tego polecenia.
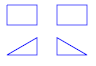
<?xml version="1.0"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1" xmlns:xlink="http://www.w3.org/1999/xlink"> <g style="stroke: blue; fill: none;"> <!-- rectangle; all four lines --> <path d="M 10 10, L 40 10, L 40 30, L 10 30, L 10 10" /> <!-- rectangle with closepath --> <path d="M 60 10, L 90 10, L 90 30, L 60 30, Z" /> <!-- two thirty-degree triangles --> <path d="M 40 60, L 10 60, L 40 42.68, Z M 60 60, L 90 60, L 60 42.68, Z" /> </g> </svg>Ostatnią ścieżkę opiszę dokładniej:
M 40 60 – startujemy w punkcie (40, 60).
L 10 60 – prowadzimy linię do (10, 60).
L 40 42.68 – prowadzimy linię do punktu (40 42.68).
Z – zamykamy ścieżkę (dorysowuje ostatnią linię do punktu (40, 60)). W ten sposób powstał pierwszy trójkąt.
M 60 60 – rozpoczynamy nową subścieżkę w punkcie (60, 60).
L 90 60 – rysujemy linię do (90, 60).
L 60 42.68 – prowadzimy linię do (60, 42.68).
Z – zamykamy ścieżkę (powstaje drugi trójkąt).
Relatywne moveto i lineto
Wszystkie komendy reprezentowane przez duże litery i występujące po nich współrzędne oznaczają współrzędne absolutne. Jeśli użyjemy małych liter komend to współrzędne będą interpretowane jako relatywne względem aktualnej pozycji pióra. Ilustruje to poniższy przykład.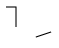
<?xml version="1.0"?> <!DOCTYPE svg PUBLIC "-//W3C//DTD SVG 1.1//EN" "http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd"> <svg xmlns="http://www.w3.org/2000/svg" version="1.1" xmlns:xlink="http://www.w3.org/1999/xlink"> <path d="M 10 10 L 20 10 L 20 30 M 40 40 L 55 35" style="stroke: black; fill: none;" /> <path d="M 10 10 l 10 0 l 0 20 m 20 10 l 15 -5" style="stroke: black; fill: none" /> </svg>Z obu ścieżek otrzymamy to samo. Aby to zobaczyć usuń najpierw pierwszą ze ścieżek zostawiając drugą, a potem odwrotnie.
Komendy horizontal lineto i vertical lineto
Horizontal lineto oznacza poziomą linię i jest reprezentowane przez komendę H dla obsolutnej współrzędnej x lub h dla relatywnej współrzędnej x. Podobnie vertical lineto (linia pionowa) jest reprezentowana przez V dla absolutnej współrzędnej y oraz v dla relatywnej. Spójrzmy na poniższą tabelkę:| Skrót | Znaczenie | Efekt |
|---|---|---|
| H 40 | L 40 aktualne_y | Rysuje linię do absolutnego położenia (40, aktualne_y) |
| h 40 | l 40 0 | Rysuje linię do (aktualne_x + 40, aktualne_y) |
| V 40 | L aktualne_x 40 | Rysuje linię do absolutnego położenia (aktualne_x, 40) |
| v 40 | l aktualne_x 40 | Rysuje linię do (aktualne_x, aktualne_y + 40) |
Elliptical Arc (eliptyczny łuk)
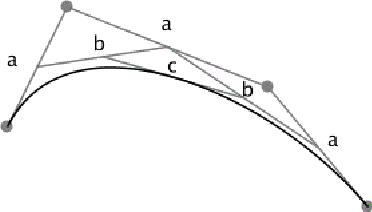
Rysowanie linii jest proste, co jednak gdy chcemy narysować krzywą łączącą dwa punkty? Takich krzywych jest nieskończenie wiele więc musimy podać określone informacje, aby można było narysować odpowiednią krzywą. Najprostszą z krzywych jest eliptyczny łuk (elliptical arc) – jest to część łuku elipsy łączący dwa jej punkty.Pierwszą częścią informacji jest określenie promieni rx i ry elipsy, na których leżą punkty początku i końca elipsy. Wskazuje to na dwie odmienne elipsy, a zarazem cztery łuki (patrz rys. a). Na rysunkach b i c łuki są mniejsze niż 180 stopni, a na d i e większe od 180 stopni. Jeśli spojrzymy na rysunki b i c zauważymy, że różnią się one kierunkiem. Podobnie jest z rysunkami d i e.
Komendy dotyczące łuku zaczynają się od A (we współrzędnych absolutnych) lub a (we współrzędnych relatywnych) i mają następujące parametry:
- rx i ry – promienie elipsy, na których leżą punkty początku i końca elipsy,
- x-axis-rotation, który wskazuje jak elipsa ma być obrócona,
- large-arc-flag – wskazuje, która część elipsy jest brana od uwagę (jeśli parameter wynosi 0 oznacza to miara kąta wycinka elipsy jest mniejsza od 180 stopni, jeśli parameter wynosi 1 to miara kąta jest większa lub równa 180 stopni),
- sweep-flag – określa kierunek kąta,
- x, y – współrzędne punktu kończącego łuk.
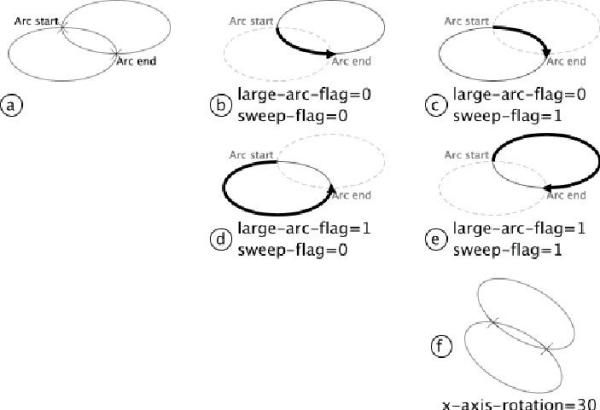 Poniższe linijki przedstawiają kod tworzący łuki eliptyczne od b do e. Poniższy rysunek pokazuje łuk b.
Poniższe linijki przedstawiają kod tworzący łuki eliptyczne od b do e. Poniższy rysunek pokazuje łuk b.

<path d="M 125,75 A100,50 0 0,0 225,125" /> <!-- b --> <path d="M 125,75 A100,50 0 0,1 225,125" /> <!-- c --> <path d="M 125,75 A100,50 0 1,0 225,125" /> <!-- d --> <path d="M 125,75 A100,50 0 1,1 225,125" /> <!-- e -->
Krzywe Beziera
Krzywa Baziera to parametryczna krzywa powszechnie stosowana w programach do projektowania inżynierskiego CAD, projektowania grafiki komputerowej (Corel Draw, Adobe Illustrator, GIMP, Inkscape), do reprezentowania obrysów znaków w fontach komputerowych (TrueType, METAFONT, Type1) i systemach przetwarzania grafiki (PostScript, MetaPost) oraz w grafice wektorowej (np. format SVG). Krzywe Béziera są krzywymi parametrycznymi - każda współrzędna punktu krzywej jest pewną funkcją liczby rzeczywistej - parametru; żeby określić krzywą na płaszczyźnie potrzebne są dwie funkcje, żeby określić krzywą w przestrzeni - trzy, itd. Ze względu na rodzaj tych funkcji mówi się o krzywych wielomianowych oraz krzywych wymiernych. Powszechnie stosuje się również krzywe złożone z kawałków gładko połączonych krzywych wielomianowych bądź wymiernych - krzywe B-sklejane (także krzywe gładkie).Niezależnie od rodzaju krzywej na jej przebieg wpływa łamana kontrolna określona za pomocą punktów kontrolnych.
Kwadratowe krzywe Beziera
Najprostszą krzywą Beziera jest kwadratowa krzywa. Trzeba dla niej określić tylko punkt początkowy, punkt końcowy i punkt kontrolny. Wyobraźmy sobie dwa ramiona namiotu umieszczone przy punktach końcowych linii. Te ramiona spotykają się w jednym punkcie nazywanym punktem kontrolnym. Linia pomiędzy środkami ramion namiotu jest ruchoma i rysuje naszą krzywą.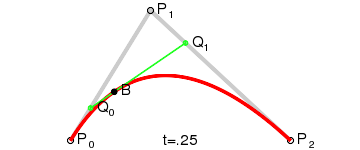 Dokładniej powyższy rysunek można opisać następująco:
Dokładniej powyższy rysunek można opisać następująco:
- punkt Q0 zmienia się od P0 do P1 i rysuje prostą P0P1 czyli liniową krzywą Beziera,
- punkt Q1 zmienia się od P1 do P2 i rysuje prostą P1P2 czyli liniową krzywą Beziera,
- punkt B(t) zmienia się od Q0 do Q1 i rysuje kwadratową krzywą Beziera (narysowana kolorem czerwonym).
Kwadratowe krzywe Beziera definiujemy za pomocą komend Q (absolutne) i q (relatywne). Poniższy kod określa kwadratową krzywą Beziera z punktu (30, 75) do (300, 120), gdzie punkt (240, 30) jest punktem kontrolnym.
<path d="M30 75 Q 240 30, 300 120" style="stroke: black; fill: none;"/>
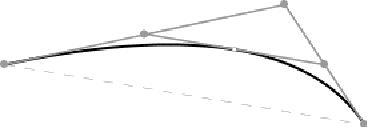 Można określić wiele zestawów współrzędnych po komendzie Q. Będzie to generować krzywą polibeziera. Spójrzmy na poniższy kod. Generuje on krzywą z punktu (30, 100)
do punktu (100, 100) z punktem kontrolnym (80, 30) i kontynuuje jej rysowanie do punktu
(200, 80) z punktem kontrolnym (130, 65). Wygląd krzywej przedstawia rysunek poniżej.
Można określić wiele zestawów współrzędnych po komendzie Q. Będzie to generować krzywą polibeziera. Spójrzmy na poniższy kod. Generuje on krzywą z punktu (30, 100)
do punktu (100, 100) z punktem kontrolnym (80, 30) i kontynuuje jej rysowanie do punktu
(200, 80) z punktem kontrolnym (130, 65). Wygląd krzywej przedstawia rysunek poniżej.

<path d="M30 100 Q 80 30, 100 100, 130 65, 200 80" style="stroke: black; fill: none;" />
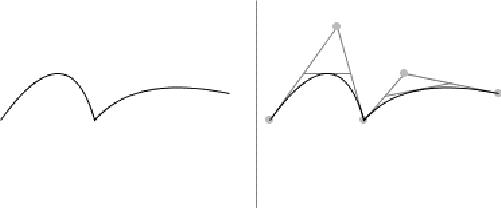 Widać, że powyższe krzywe są połączone ostrym kantem. Co zrobić aby krzywa była gładka? SVG daje nam komendę T (lub t w współrzędnych relatywnych) czyli
gładką kwadratową krzywą. Poniższy kod rysuje kwadratową krzywą Beziera od punktu (30, 100) do (100, 100) z punktem kontrolnym (80, 30) i gładko kontynuowana
do (200, 80). Efekt widzimy na rysunku poniżej.
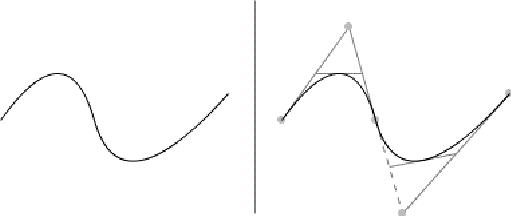
Widać, że powyższe krzywe są połączone ostrym kantem. Co zrobić aby krzywa była gładka? SVG daje nam komendę T (lub t w współrzędnych relatywnych) czyli
gładką kwadratową krzywą. Poniższy kod rysuje kwadratową krzywą Beziera od punktu (30, 100) do (100, 100) z punktem kontrolnym (80, 30) i gładko kontynuowana
do (200, 80). Efekt widzimy na rysunku poniżej.
<path d="M30 100 Q 80 30, 100 100 T 200 80" />
Sześcienne krzywe Beziera
Pojedyncza kwadratowa krzywa Beziera posiada dokładnie jeden punkt załamania (punkt, w którym krzywa zmienia kierunek). Sześcienne krzywe Beziera mogą mieć jeden lub dwa punkty załamania. Kolejną różnicą pomiędzy kwadratową a sześcienną krzywą Beziera jest to, że krzywa sześcienna posiada dwa punkty kontrolne (po jednym dla każdego punktu końcowego). Technika tworzenia sześciennej krzywej jest podobna do tworzenia kwadratowej krzywej. Przykład sześciennej krzywej Beziera przedstawia poniższy rysunek. Przykład tworzenia poniżej.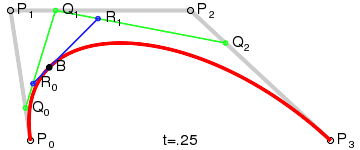 Opiszę pokrótce konstrukcję powyższej krzywej. Jak widać mamy trzy punkty Q0, Q1 i Q2, które zmieniają się od P0
do P1, P1 do P2 i P2 do P3
odpowiednio i rysują linie (liniowe krzywe Beziera). Natomiast punkty R0 i R1 zmieniają się od Q0 do Q1 i Q1 do Q2 odpowiednio
i rysują sześcienną krzywą Beziera.
Opiszę pokrótce konstrukcję powyższej krzywej. Jak widać mamy trzy punkty Q0, Q1 i Q2, które zmieniają się od P0
do P1, P1 do P2 i P2 do P3
odpowiednio i rysują linie (liniowe krzywe Beziera). Natomiast punkty R0 i R1 zmieniają się od Q0 do Q1 i Q1 do Q2 odpowiednio
i rysują sześcienną krzywą Beziera. Do określenia w SVG krzywej sześciennej (cubic curve) używamy komendy C lub c. Komenda ta określa trzy zestawy współrzędnych: punkt kontrolny dla punktu startowego, punkt kontrolny dla punktu końcowego i punkt końcowy. Poniższy kod przedstawia sześciennę krzywą Beziera startującą w punkcie (20 , 80) i kończącą się w punkcie (200, 120) z punktami kontrolnymi (50, 20) i (150, 60).
<path d="M20 80 C 50 20, 150 60, 200 120" style="stroke: black; fill: none;"/>
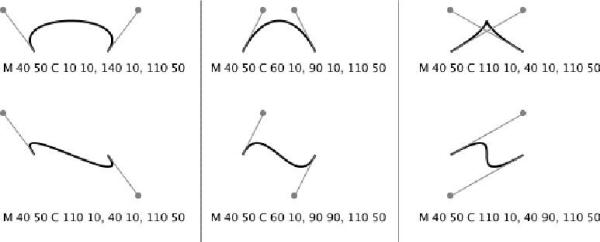
 Możesz narysować wiele interesujących krzywych. Wszystko zależy od relacji miedzy punktami kontrolnymi (patrz rysunek poniżej).
Możesz narysować wiele interesujących krzywych. Wszystko zależy od relacji miedzy punktami kontrolnymi (patrz rysunek poniżej).
 Tak jak dla kwadratowej krzywej można określić sześcienną krzywą polibeziera, określając kilka zestawów współrzędnych w komendzie C.
Ostatni punkt pierwszej krzywej staje się pierwszym punktem kolejnej itd. Spójrzmy na poniższy kod.
Tak jak dla kwadratowej krzywej można określić sześcienną krzywą polibeziera, określając kilka zestawów współrzędnych w komendzie C.
Ostatni punkt pierwszej krzywej staje się pierwszym punktem kolejnej itd. Spójrzmy na poniższy kod.

<path d="M30 100 C 50 50, 70 20, 100 100, 110, 130, 45, 150, 65, 100" style="stroke: black; fill: none;" />Generuje on sześcienną krzywą polibeziera. Zaczynamy od punktu (30, 100) i rysujemy krzywą sześcienną do (100, 100) z punktami kontrolnymi (50, 50) i (70, 20), następnie kontynuujemy do punktu (65, 100) z punktami kontrolnymi (110, 130) oraz (45, 150). Efekt jest pokazany na rysunku poniżej.
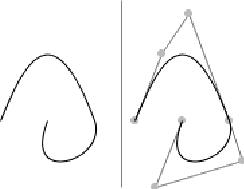 Jeśli chcesz zagwarantować sobie gładkie połączenia pomiędzy krzywymi możesz uzyć komendy S (lub s dla współrzędnych relatywnych).
To jest sześcienna krzywa prowadzona od (30, 100) do (100, 100) z punktami kontrolnymi (50, 30), (70, 50) i gładko kontynuowana do punktu (200, 80),
używając (150, 40) jako końcowego punktu kontrolnego.
Jeśli chcesz zagwarantować sobie gładkie połączenia pomiędzy krzywymi możesz uzyć komendy S (lub s dla współrzędnych relatywnych).
To jest sześcienna krzywa prowadzona od (30, 100) do (100, 100) z punktami kontrolnymi (50, 30), (70, 50) i gładko kontynuowana do punktu (200, 80),
używając (150, 40) jako końcowego punktu kontrolnego.
<path d="M30 100 C 50 30, 70 50, 100 100 S 150 40, 200 80" style="stroke: black; fill: none;" />

Ścieżki i wypełnienia
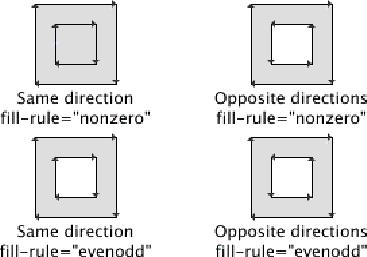
Rozważmy dwie ścieżki. Obydwie wstawiają kwadraty. W pierwszej ścieżce obydwa kwadraty są rysowane zgodnie z ruchem wskazówek zegara, natomiast w drugiej ścieżce zewnętrzny kwadrat jest rysowany zgodnie z ruchem wskazówek zegara, a wewnętrzny przeciwnie.<path d="M 0 0, 60 0, 60 60, 0 60 Z M 15 15, 45 15, 45 45, 15 45Z"/> <path d="M 0 0, 60 0, 60 60, 0 60 Z M 15 15, 15 45, 45 45, 45 15Z"/>Poniższy rysunek przedstawia różnicę w wyborze opcji wypełnienia (fill-rule).
Element <marker>
Na początek rozważmy następującą ścieżkę:<path d="M 10 20 100 20 A 20 30 0 0 1 120 50 L 120 110" style="fill: none; stroke: black;"/>Teraz dodamy do niej kółko na początku ścieżki, czarny trójkąt na końcu i strzałki wewnątrz jak na rysunku poniżej.
 Aby tego dokonać musimy utworzyć elementy <marker> i przekazać je ścieżce za pomocą referencji. Element <marker> umieszczamy wewnątrz znacznika <defs>.
Ponadto określamy jego wysokość (markerHeight) i szerokość (markerWidth). Jeśli chcemy by nasze kółko było na początku ścieżki musimy użyć
atrybutu style="marker-start: url(#mCircle), gdzie mCircle jest identyfikatorem naszego markera.
Aby tego dokonać musimy utworzyć elementy <marker> i przekazać je ścieżce za pomocą referencji. Element <marker> umieszczamy wewnątrz znacznika <defs>.
Ponadto określamy jego wysokość (markerHeight) i szerokość (markerWidth). Jeśli chcemy by nasze kółko było na początku ścieżki musimy użyć
atrybutu style="marker-start: url(#mCircle), gdzie mCircle jest identyfikatorem naszego markera.
<defs> <marker id="mCircle" markerWidth="10" markerHeight="10"> <circle cx="5" cy="5" r="4" style="fill: none; stroke: black;"/> </marker> </defs> <path d="M 10 20 100 20 A 20 30 0 0 1 120 50 L 120 110" style="marker-start: url(#mCircle); fill: none; stroke: black;"/>Jak widać na rysunku poniżej efekt odbiega od zamierzonego.
 Powodem, dla którego kółko znajduje się w złym miejscu jest to, że domyślnie punkt początkowy markera (0, 0) (start-marker) jest wyrównany do początku
współrzędnej ścieżki. Poniższy przykład dodaje atrybuty refX i refY, które mówią jakie współrzędne (w systemie markera) są wyrównane z początkiem współrzędnej ścieżki.
Powodem, dla którego kółko znajduje się w złym miejscu jest to, że domyślnie punkt początkowy markera (0, 0) (start-marker) jest wyrównany do początku
współrzędnej ścieżki. Poniższy przykład dodaje atrybuty refX i refY, które mówią jakie współrzędne (w systemie markera) są wyrównane z początkiem współrzędnej ścieżki.
<marker id="mCircle" markerWidth="10" markerHeight="10" refX="5" refY="5"> <circle cx="5" cy="5" r="4" style="fill: none; stroke: black;"/> </marker>
 Dodamy teraz kolejne marker. Czarny trójkąt ma być ustawiony na końcu ścieżki, więc użyjemy atrybutu marker-end: url(#mTriangle),
gdzie mTriangle jest identyfikatorem markera (czarnego trójkąta). Strzałki wewnątrz ścieżki dodamy za pomocą marker-mid.
Dodamy teraz kolejne marker. Czarny trójkąt ma być ustawiony na końcu ścieżki, więc użyjemy atrybutu marker-end: url(#mTriangle),
gdzie mTriangle jest identyfikatorem markera (czarnego trójkąta). Strzałki wewnątrz ścieżki dodamy za pomocą marker-mid.
<defs> <marker id="mCircle" markerWidth="10" markerHeight="10" refX="5" refY="5"> <circle cx="5" cy="5" r="4" style="fill: none; stroke: black;"/> </marker> <marker id="mArrow" markerWidth="6" markerHeight="10" refX="0" refY="4"> <path d="M 0 0 4 4 0 8" style="fill: none; stroke: black;"/> </marker> <marker id="mTriangle" markerWidth="5" markerHeight="10" refX="5" refY="5"> <path d="M 0 0 5 5 0 10 Z" style="fill: black;"/> </marker> </defs> <path d="M 10 20 100 20 A 20 30 0 0 1 120 50 L 120 110" style="marker-start: url(#mCircle); marker-mid: url(#mArrow); marker-end: url(#mTriangle); fill: none; stroke: black;"/>
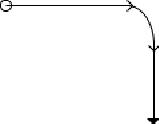
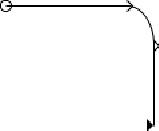 Jak widać na powyższym rysunku wynik jeszcze nie jest zadowalający. Aby otrzymać zamierzony efekt musimy jeszcze ustawić atrybut orient markera na auto.
Spowoduje to automatycznie obrócenie markerów w kierunku ścieżki.
Jak widać na powyższym rysunku wynik jeszcze nie jest zadowalający. Aby otrzymać zamierzony efekt musimy jeszcze ustawić atrybut orient markera na auto.
Spowoduje to automatycznie obrócenie markerów w kierunku ścieżki.
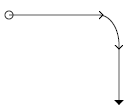
<defs> <marker id="mCircle" markerWidth="10" markerHeight="10" refX="5" refY="5"> <circle cx="5" cy="5" r="4" style="fill: none; stroke: black;"/> </marker> <marker id="mArrow" markerWidth="6" markerHeight="10" refX="0" refY="4" orient="auto"> <path d="M 0 0 4 4 0 8" style="fill: none; stroke: black;"/> </marker> <marker id="mTriangle" markerWidth="5" markerHeight="10" refX="5" refY="5" orient="auto"> <path d="M 0 0 5 5 0 10 Z" style="fill: black;"/> </marker> </defs> <path d="M 10 20 100 20 A 20 30 0 0 1 120 50 L 120 110" style="marker-start: url(#mCircle); marker-mid: url(#mArrow); marker-end: url(#mTriangle); fill: none; stroke: black;"/>Powyższy kod generuje ścieżkę z markerami, taką jak na pierwszym rysunku w niniejszym paragrafie.
