Implicit equation grapher i marching cubes
Niedawno przygotowałam kolejny program w webgl (three.js) rysujący wykresy powierzchni 3d. Tym razem zadanych równaniem uwikłanym typu f(x,y,z) = 0. Właśnie w przypadku takich równań trzeba użyć algorytmu przybliżającego strukturę powierzchni. Idealnym do tego celu jest algorytm maszerujących sześcianów (marching cubes). Marching cubes dla określonego przestrzennego pola skalarnego tworzy siatkę wielokątów przybliżającą naszą powierzchnię. Rozbudowany opis tego algorytmu można znaleźć na stronie Paula Bourke. Opiera on swe działanie prawie wyłącznie na indeksowaniu predefiniowanych tablic (tzw. lookup tables). Wykorzystałam tablice przygotowane specjalnie dla javascriptu przez alteredq.
 Rys. 1 źródło zdjęcia: Wikipedia
Rys. 1 źródło zdjęcia: WikipediaPodstawowym problemem jest stworzenie przybliżenia powierzchni izoskalarnej pola skalarnego próbkowanego w regularnej trójwymiarowej siatce. Gdy mamy jedną komórkę siatki próbkowania tzw. woksel (kostka) – zdefiniowaną przez jej wierzchołki oraz wartości pola skalarnego w każdym z wierzchołków, można stworzyć układ płaskich wielokątów, który najlepiej opisuje izopowierzchnię, która przechodzi (lub nie) przez komórki owej przestrzennej siatki próbkowania. Izopowierzchnia może przechodzić (lub nie) przez woksel oraz może przechodzić na jeden z wielu sposobów. Każdy taki przypadek będzie określony poprzez liczbę wierzchołków, które są obejmowane lub nie przez powierzchnię. Mówimy, że jeśli wartość pola w wierzchołku jest mniejsza od stałej wartości pola na izopowierzchni – izowartości – to wierzchołek leży pod izopowierzchnią, w innym przypadku leży ponad nią. Zatem jeśli jeden z wierzchołków jest ponad izopowierzchnią i powiedzmy naprzeciwległy wierzchołek leży pod nią, to wiemy, że izopowierzchnia wycina krawędź pomiędzy tymi wierzchołkami. Miejsce, w którym powierzchnia przecina krawędź elementarnego sześcianu wyznaczane jest poprzez interpolację liniową, tzn. zakładamy, że stosunek długości odcinków od punktu przecięcia boku komórki z izopowierzchnią do pierwszego i drugiego wierzchołka, będzie taki sam jak stosunek wartości powierzchni w punkcie przecięcia do wartości pola skalarnego w pierwszym i drugim wierzchołku. Sposób numerowania wierzchołków i krawędzi użyty w algorytmie jest przedstawiony na rysunku:
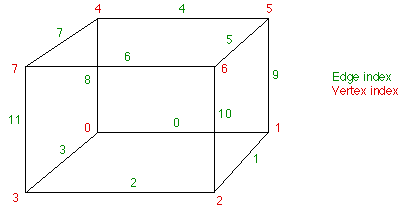 Rys. 2 źródło zdjęcia: Paul Bourke
Rys. 2 źródło zdjęcia: Paul BourkePrzykładowo jeśli wartość w wierzchołku trzecim jest mniejsza od izowartości i wszystkie wartości, we wszystkich innych wierzchołkach są większe od izowartości, wówczas stworzylibyśmy trójkątną ściankę odcinającą wierzchołki 2,3 i 11. Odpowiada to sytuacji drugiej od lewej w pierwszym rzędzie na rys. 1. Dokładna pozycja wierzchołków tej ścianki, na odcinkach 3-2, 3-0, 3-7, zależy od stosunku izowartości do wartości pola skalarnego w wierzchołkach sześcianu (wspomniana wcześniej interpolacja liniowa).
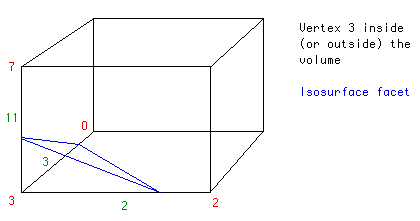 Rys. 3 źródło zdjęcia: Paul Bourke
Rys. 3 źródło zdjęcia: Paul BourkeNajpierw należy użyć tablicy edgeTable, która przyporządkowuje wierzchołki pod powierzchnią do przecinanych krawędzi. Na początku tworzony jest ośmiobitowy indeks, w którym każdy bit odpowiada wierzchołkowi.
var cubeidx = 0, isolvl = 0; if(val0 < isolvl) cubeidx |= 1; if(val1 < isolvl) cubeidx |= 2; if(val2 < isolvl) cubeidx |= 8; if(val3 < isolvl) cubeidx |= 4; if(val4 < isolvl) cubeidx |= 16; if(val5 < isolvl) cubeidx |= 32; if(val6 < isolvl) cubeidx |= 128; if(val7 < isolvl) cubeidx |= 64;Następnie przeszukujemy tablicę krawędzi, która jest tak skonstruowana, że każdej z wartości indeksu cubeidx odpowiada dwunastobitowy numer, w którym każdy bit charakteryzuje stan poszczególnych krawędzi: 0 jeśli krawędź nie jest przecinana przez powierzchnię, 1 jeśli krawędź jest przecinana przez powierzchnię. Jeżeli żadna z krawędzi nie jest przecinana tablica zwraca po prostu 0, co ma miejsce, gdy współczynnik cubeidx równy jest 0 (wszystkie współczynniki poza powierzchnią) lub 0xff (wszystkie współczynniki pod powierzchnią). Używając przykładu z rys. 3, gdzie jedynie wierzchołek 3 ma wartość mniejszą od izowartości, cubeidx byłby równy dwójkowo 0000 1000 lub dziesiętnie 8. Wówczas wartości edgeTable[8] = 0x80c = (1000 0000 1100)2. Co oznacza, że krawędzie 2,3, i 11 czyli odpowiadające ustawionym bitom, są przecinane przez izopowierzchnię. Dla wszystkich przeciętych krawędzi, za pomocą interpolacji liniowej, wyznaczane są punkty przecięcia. Jeśli P1 i P2 są wierzchołkami przeciętej krawędzi oraz V1 i V2 są wartościami pola skalarnego w każdym z tych wierzchołków, to punkt przecięcia P wyliczany jest za pomocą następującego równania: P = P1 + (izowartość - V1) (P2 - P1) / (V2 - V1) Ostatnia część algorytmu marching cubes wymaga skonstruowania poprawnej i jednoznacznej reprezentacji wielokątowej w oparciu o informacje uzyskane z wyznaczonych przecięć izopowierzchni z krawędziami komórki próbkowania. Tym razem wykorzystywana jest druga tablica triTable, której indeksem jest wartość cubeidx, a wartością sekwencja wierzchołków trójkątów (tylu na ile konieczne by poprawnie reprezentować powierzchnię w komórce siatki). Maksymalnie może być aż 5 trójkątów. W poprzednim kroku wyznaczyliśmy punkty przecięcia wzdłuż krawędzi 2,3 i 11. Ósmy (cubeidx=8) element tablicy triTable wygląda następująco: {3, 11, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1} Za pomocą tablicy triTable budujemy już konkretne trójkąty.
var i = 0;
cubeidx *= 16;
while(THREE.triTable[cubeidx + i] != -1)
{
var idx1 = THREE.triTable[cubeidx + i];
var idx2 = THREE.triTable[cubeidx + i + 1];
var idx3 = THREE.triTable[cubeidx + i + 2];
geom.vertices.push(vlist[idx1].clone());
geom.vertices.push(vlist[idx2].clone());
geom.vertices.push(vlist[idx3].clone());
geom.faces.push(new THREE.Face3(vidx, vidx+1, vidx+2));
geom.faceVertexUvs[0].push([new THREE.Vector2(0,0), new THREE.Vector2(0,1), new THREE.Vector2(1,1)]);
vidx += 3;
i += 3;
}
W przykładzie 3d graphera w javascripcie (three.js) najpierw budujemy tablicę punktów i ich wartości. Zmienna size to ilość kostek na jaką dzielimy siatkę - określa niejako dokładność przybliżenia. Im mniejsza tym algorytm będzie mniej dokładny. Przy size = 40, będziemy mieli 64000 punktów.
var points = [], vals = [], size = 40, n = 0, j = 0, i = 0;
for(n = 0; n < size; n++)
for(j = 0; j < size; j++)
for(i = 0; i < size; i++)
{
var x = axisMin1 + axisRange1 * i / (size - 1);
var y = axisMin2 + axisRange2 * j / (size - 1);
var z = axisMin3 + axisRange3 * n / (size - 1);
points.push(new THREE.Vector3(10*x,10*y,10*z));
var value = f(x, y, z);
vals.push(value);
}
Dopiero później przechodzimy do algorytmu maszerujących sześcianów opisanego wyżej.
Poniżej przykładowe powierzchnie wygenerowane przez algorytm.

 Źródła:
Źródła:http://paulbourke.net/geometry/polygonise/
http://pl.wikipedia.org/wiki/Marching_cubes
http://www.cs.carleton.edu/cs_comps/0405/shape/marching_cubes.html
http://www.ia.hiof.no/~borres/cgraph/explain/marching/p-march.html
http://mipav.cit.nih.gov/pubwiki/index.php/Extract_Surface_(Marching_Cubes)
http://threejs.org/examples/webgl_marching_cubes.html
